Dont Need to Randomize Again Experiment
Must Nosotros Randomize Our Experiment?
Report No. 47
George Box
Copyright © 1989, Used past Permission
Applied Significance
The importance of randomization in the running of valid experiments in an industrial context is sometimes questioned. In this written report the essential bug are discussed and guidance is provided.
Keywords: Randomization, Non-stable Systems, Nonstationarity, Design of Experiments
*This report will appear as #2 in the serial to be called "George's Column" in the Journal of Qualily Engineering science (1990).
"My guru says you must always randomize."
"My guru says y'all don't need to."
"You should never run an experiment unless you are certain the system (the process, the pilot plant, the lab operation) is in a country of control."
"Randomization would make my experiment incommunicable to run."
"I took a grade in statistics and all the theory worked out perfectly without any randomization."
We have all heard statements like these. What are nosotros to conclude?
The Problem of Running Experiments in the Real Globe
The statistical design of experiments was invented almost lxx years ago past Sir Ronald Fisher. His objective was to brand it possible to run informative and unambiguous experiments not just in the laboratory simply in the existent world outside the laboratory. Initially his experimental material was agricultural land. Not simply did this state vary a peachy bargain as you lot went from one experimental plot to the adjacent, merely the yields from successive plots were related to each other. Suppose that if no treatment was practical so that the "disturbance" you saw was simply "mistake", then the yields from successive plots would non look like the random stationary disturbance (Due south) in the effigy, which is a picture of an platonic process in a state of control with results varying randomly about a fixed mean. Instead they might wait like the non-stationary process N where a high yielding plot was likely to be followed by another loftier yielding plot and visa versa. And then the background disturbance against which the effect of dissimilar treatments had to be judged varied in a highly non-random - unstable - non-stationary way. Fisher'south problem was how to run valid comparative experiments in this state of affairs.
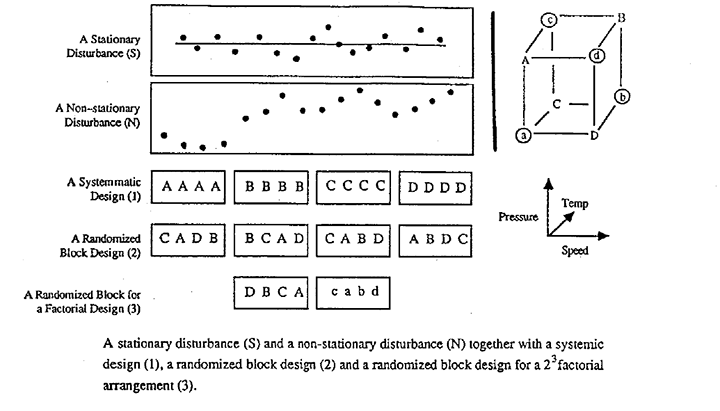
Is Your Experimental System in a Land of Statistical Control?
The problem that Fisher considered is not confined to agricultural experimentation. To see if y'all believe in random stationarity in your particular kind of work, call back of the size of chance differences you expect in measurements taken m steps autonomously (in time or in space). Random variation about a fixed mean implies that the variation in such differences remains the aforementioned whether the measurements are taken ane step autonomously or ane hundred steps apart. If you lot believe instead the variation would, on the average, continually increase as the distance apart became greater, and so you don't believe in starionarity.*
The truth is that we all live in a not-stationary world; a world in which external factors never stay still. Indeed the idea of stationarity - of a stable globe in which, without our intervention, things stay put over time - is a purely conceptual 1. The concept of stationarity is useful only as a background against which the real not-stationary world tin be judge. For example, the manufacture of parts is an operation involving machines and people. Simply the parts of a machine are not fixed entities. They are wearing out, changing their dimensions, and losing their adjustment. The beliefs of the people who run the machines is non fixed either. A single operator forgets things over time and alters what he does. When a number of operators are involved, the opportunities for change because of failures to communicate are further multiplied. Thus, if left to itself whatsoever process will drift away from its initial state. It would be overnice if uniformity could be achieved, once and for all, by advisedly adjusting a machine, giving appropriate instructions to operators, and letting it run, merely unfortunately this would rarely, if ever, result in the production of uniform product. Extraordinary precautions are needed in exercise to ensure that the system does not drift away from the target value and that it behaves like the stationary procedure (S).
So the start thing we must empathise is that stationarity, and hence the uniformity of everything depending on it, is an unnatural land that requires a slap-up deal of effort to achieve. That is why good quality control takes and then much try and is so important. All of this is truthful, not just for manufacturing processes, but for any operation that we would like to be done consistently, such every bit the taking of claret pressures in a hospital or the performing of chemical analyses in a laboratory. Having found the best way to practice it, nosotros would similar it to be done that way consistently, just feel shows that very careful planning, checking, recalibration and sometimes advisable intervention, is needed to ensure that this happens.
*Standard courses in mathematical statistics accept not helped, since they frequently assume a stationary disturbance. Specifically, they commonly suppose that the disturbance consists of errors that vary independently about a stock-still mean or about a fixed model. Studies of the effects of discrepancies from such a model have usually concerned such questions every bit what would happen if the information followed a not-normal (but still stationary) process. However, discrepancies due to non-normality are usually trivial compared with those arising from non-stationarity.
Performing Experiments in a Nonstationary Surroundings
And then what did Fisher suggest we do about running experiments in this non-stationary world? For illustration suppose we had 4 different methods/treatments/procedures (A, B, C, and D) to compare, and we wanted to test each method iv times over. Fisher suggested that rather than run a systematic design like Design 1 in Effigy ane, in which we get-go ran all the A's, then all the B'southward and so on, we should run a "randomized block" arrangement like Design 2. In this latter arrangement inside each "block" of four yous would run each of the treatments A, B, C, and D in random society. *
* [footnote in printed report] The idea of getting rid of external variation past blocking has other uses. The blocks might refer, non to runs made at unlike periods of fourth dimension, but to runs made on different machines, or to runs made with different operators. In each instance randomization within the blocks would validate the experiment, the subsequent analysis, and the conclusions.
Now frequently Pattern one would be a lot easier to run than Design 2, so it is reasonable to ask "What does Design 2 practice for me that Design 1 doesn't?" Well, if nosotros could be absolutely sure that the process disturbance was like S - that throughout the experiment the process was in a perfect state of control with variation random about a stock-still mean, then information technology would make absolutely no departure which blueprint was used. In this example Designs ane and ii would be every bit practiced.
But suppose the process disturbance was non-stationary like that marked N in Effigy i. Then it is easy to meet that the systematic Design 1 would give invalid results. For example even if the different treatments actually had no result B, C, and D could look very skilful compared with A but because the process disturbance happened to be "upwardly" during the dine when the B, C and D runs were being made. On the other hand, if the experiment were run with the randomized Design two it would provide valid comparisons of A, B, C and D. As well, the standard methods of statistical analysis would be approximately valid even though they were based on the usual assumptions, including stationarity; that is, the information could be analyzed as if the procedure had been in a state of command. Not just this, but differences in block averages, which could account for a lot of the variation, would be totally eliminated and the relevant experimental error would be only that which occurred between plots in the same cake.
If the experiment was not simply a comparison of unlike methods similar A, B, C and D, but a factorial design like the 1 in the right of the figure in which speed, pressure and temperature were being tested, you could even so apply the same idea. As in Design 3, you could put the factorial runs marked A, B, C, and D in the first block and those labeled a, b, c and d in the second. In both cases you would run in random lodge within the blocks. It would and so again plough out that you could calculate the usual contrasts for all the main effects and all the two-factor interactions free from differences betwixt blocks and that you could carry out a standard assay every bit if the process had been in a state of control throughout the experiment, if the details of these ideas are unfamiliar, you lot tin can discover out more virtually them in any proficient book on experimental design.
Randomized experiments of this kind fabricated it possible for the kickoff time to deport valid comparative experiments in the real world outside the laboratory. Thus beginning in the 1920'due south, valid experimentation was possible not simply in agriculture, only also in medicine, biology, forestry, drug testing, stance surveys, and so along. Fisher's ideas were rapidly introduced into all these areas.
Comparative Experiments
Why do I go on using the term comparative experiments? Experimentation in a non-stationary environment cannot claim to tell united states of america what is the precise result of using, say, treatment A. This must depend to some extent on the country of the environs at the particular time of the experiment (for example, in the agricultural experiment, it would depend on the fertility of the particular soil on which treatment A was tested). What information technology can exercise is to brand valid comparisons that are probable to hold upward in similar circumstances of experimentation.* This is usually all that is needed.
Beginning in the 1930's and 1940's these ideas of experimental design also began to exist used in industrial experiments both in Britain and in the U.South. Other designs were developed in England and America in the 1940'south and 1950's such as fractional factorial designs and other orthogonal arrays and also variance component designs and response surface designs to run into new problems. These were used specially in the chemical industry. In all of this, Fisher's basic ideas of randomization and blocking retained their importance because most of the time ane could not exist sure that disturbances were even approximately in a country of statistical control.
Until fairly recently in this state experimental blueprint had not been used extensively in the "parts" industries (e. thou. automobile manufacture for example). Now, withal, because of its use by the Japanese, who borrowed these concepts from the West, some of the ideas of experimental blueprint are beingness re-imported from Japan. In particular this is true of the and so-chosen "Taguchi methods". These methods pay scant attention to randomization and blocking however. So the question is often raised equally to whether or not randomization is withal of import in the "parts" industries.
* [footnote] Notation that the question of what are similar circumstances of experimentation must invariably rest on the technical stance of the person using the results. It is not a statistical question, every bit has been pointed out by Deming (1950, 1975) in his discussion of enumerative and analytic studies.
What to Practice
To empathise what we should do in exercise, let'due south look at the trouble a niggling more closely. Nosotros have seen that we live in a non-stationary world in which cypher stays put whether we are talking about the process of manufacturing or the taking of a blood pressure reading. Simply all models are approximations, then the real question is whether the stationary approximation is skilful enough for your item situation. According to my argument, if it is, you lot don't need to randomize. Such questions are not easy - for while the degree of non-stationary in making parts, a for example, usually is very different from that occurring in an agronomical field, the precision needed in making a part is correspondingly much greater and the differences nosotros may be looking for, much smaller. Also fifty-fifty in the automobile industry not all problems are about making parts.
Many experiments (for instance, those arising in the paint shop) are conducted in circumstances much less easy to control.
The crucial factor in the effective use of any statistical method is good judgement. All I can do hither is to aid y'all employ it, and in particular to make clear what information technology is you must use your good judgement almost.
All correct so. Y'all exercise not need to randomize if you believe your system is, to a sufficiently proficient approximation, in a state of command and can be relied on to stay in that land while you make experimental changes (that presumably y'all have never made before). Sufficiently expert approximation to a state of control means that over the menstruation of experimentation differences due to the slight caste of non-stationarity existing will exist small compared with differences due to the treatments. In making such a judgment deport in mind that belief is not the same as wishful thinking.
My advice and so would be:
- In those cases where randomization only slightly complicates the experiment, always randomize.
- In those cases where randomization would make the experiment impossible or extremely hard to do, but you can make an honest judgement about estimate stationarity of the kind outlined to a higher place, run the experiment anyway without randomization.
- if you believe the process is then unstable that without randomization the results would be useless and misleading, and randomization would brand the experiment impossible or extremely hard to do, and then exercise not run the experiment. Work instead on stabilizing the process or on getting the information some other fashion.
- A compromise pattern that sometimes helps to overcome some of these difficulties is the split plot organisation. Maybe I can talk to you lot about this in a later column.
References
- Deming, Westward.E. (1950). Some Theory of Sampling, New York: Wiley.
- Deming, W.Eastward. (1975). On Probability as a Footing for Action, American Statistician, Vol. 29, No. 4, pp. 146-152.
Source: https://williamghunter.net/george-box-articles/must-we-randomize-our-experiment